IR-Spektroskopie (mittleres Infrarot) umfasst die Spektralbereiche der elektromagnetischen Strahlung
| 400...4000 cm-1 | |
| 25...2,5 µm | |
| 12...120 THz | |
| 50...500 meV |
Ein Moment ist allgemein das Produkt zweier physikalischer Größen, von denen eine die Dimension der Länge hat. Dafür gibt es verschiedene Beispiele.
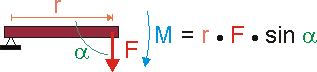
So ist das Drehmoment M das Moment einer Kraft F, die vermittels eines Hebels der Länge r als "Drehkraft" auf den Lagerpunkt dieses Hebels wirkt. Und genau so, wie eine Kraft auf einen Körper beschleunigend wirkt, wirkt das Drehmoment auf die Rotation des Hebels beschleunigend.
Im Falle mehrerer, starr verbundener Hebelarme (z.B. Wägebalken) addieren sich natürlich die einzelnen Drehmomente zum Gesamtdrehmoment. Man beachte dabei (siehe Bild) das negative Vorzeichen von r2.
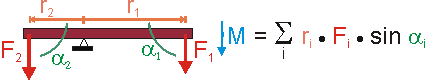
Betrachten wir nun einen Balken ohne Auflagepunkt, der frei beweglich ist.
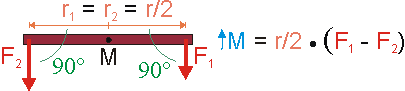
In diesem Fall ersetzt der Massenmittelpunkt des Balkens das Lager. Er liegt im Beispiel in der Mitte des Balkens. Die Radien besitzen dann gleiche Länge, aber entgegengesetztes Vorzeichen. Im Produkt des Drehmoments kann man das negative Vorzeichen auch der Kraft zuordnen und den Radius positiv lassen. Beide Radien sind dann gleich und können ausgeklammert werden. Als Resultat wirkt die Differenz der Kräfte als Drehmoment beschleunigend im Sinne der Rotation des Balkens um den Massenmittelpunkt. Der Mittelwert der Kräfte hingegen wirkt beschleunigend im Sinne der Translation und greift am Massenmittelpunkt an.
Nach diesen Mechanikexkurs wenden wir uns nun der Ladung zu. Ganz analog verhalten sich elektrische Kräfte an "starr" verbundenen Ladungen.
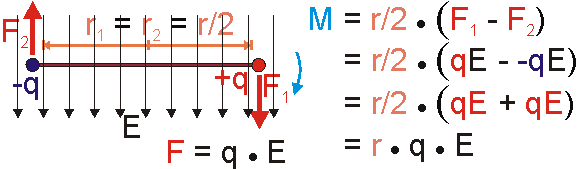
Die durch das elektrische Feld verursachten Kräfte ergeben sich jeweils als Produkt aus Ladung und Feldstärke. Setzt man dies in die Gleichung des Drehmoments ein und formt etwas um (siehe Bild), so ergibt sich als resultierendes Drehmoment ein Produkt aus der Ladung q, dem Abstand r und der elektrischen Feldstärke E. Ladung und Abstand lassen sich bezüglich des elektrischen Felds zum Moment des Dipols, dem Dipolmoment, zusammenfassen. Im Ergebnis dreht sich der Dipol, er richtet sich in Feldrichtung aus. Da beide Ladungen den gleichen Betrag und entgegengesetzte Polarität besitzen, sind auch beide Kräfte gleich groß und entgegengesetzt gerichtet. Die Summe der Kräfte verschwindet, eine translatorische Bewegung wird deshalb nicht verursacht. Das lässt sich auch daraus erklären, dass der hier betrachtete Dipol als Ganzes elektrisch neutral ist und deshalb von Feld nicht translatorisch bewegt wird.
Die im Bild gezeigte Anordnung zweier entgegengesetzt polarer Ladungen wird auch als Dipol bezeichnet. Das Produkt des Betrags entgegengesetzt polarer Ladungen q und des Abstands r definieren das Dipolmoment p.
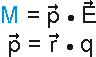
Eingesetzt in die Gleichung des Drehmoments M ergibt sich die Beschreibung der Wirkung eines elektrischen Felds auf einen Dipol: Der Dipol erfährt eine Kraft, die Ihn in Feldrichtung beschleunigt und ausrichtet. Durch den vektoriellen Charakter der Größen wird allgemein der Fall berücksichtigt, dass abweichend von den gezeigten Anordnungen die Kräfte bzw. das elektrische Feld nicht senkrecht zur Anordnung angreifen.
Allgemein beschreibt das Dipolmoment die Ungleichverteilung der Ladung unter Berücksichtigung ihres Abstands. Mit Hilfe des Dipolmoments lassen sich nicht nur (aber auch) die eine Rotation verursachenden Kräfte beschreiben.
Dipolare Moleküle oder Molekülgruppen sind dadurch gekennzeichnet, dass sich in ihnen die positive Ladung (der Kerne) und die negative Ladung (der Elektronen) nicht gleichmäßig verteilen. Sie verhalten sich adäquat und lassen sich ebenfalls durch das Dipolmoment beschreiben. Betrachten wir dazu als Beispiel die Ladungsverteilung eines Wassermoleküls.
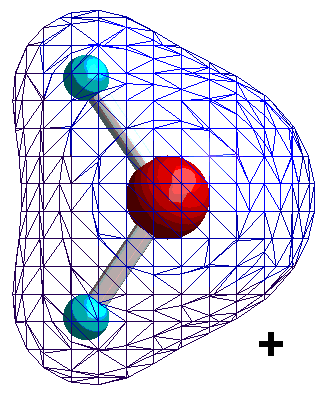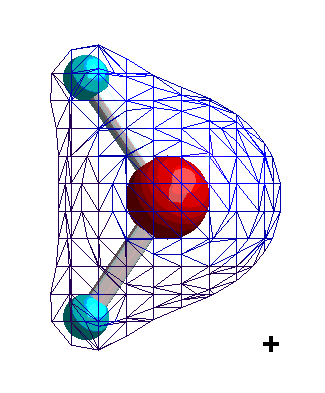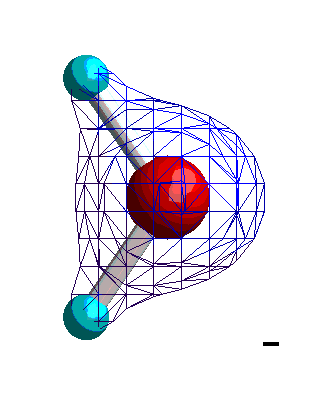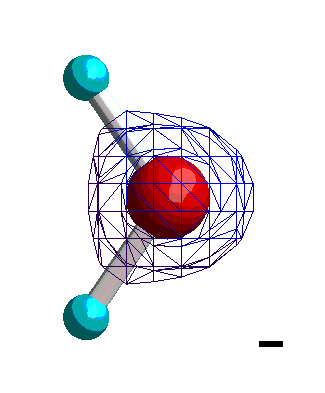 |
Isocharge-Flächen quantenmechanisch berechnet Methode: restricted Hartree-Fock Basissatz: 6-31G |

Abstrahieren wir nun zum Dipol:
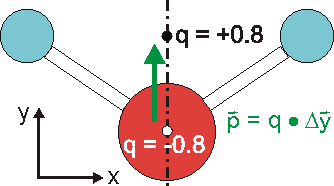
Die Ladungsverteilung des Wassers ist in x-Richtung völlig symmetrisch, wobei die Strichpunktlinie die Symmetrieachse ist. Deshalb heben sich alle Ladungsungleichgewichte bezüglich der x-Richtung auf. In y-Richtung verbleibt ein "Ladungsungleichgewicht", das sich durch die Projektion aller Ladungen auf die Symmetrieachse und deren Abstand beschreiben lässt. Das Dipolmoment ist dann ein Vektor, der dem Produkt aus Ladung und Abstand entspricht und von der negativen zur positven Ladung gerichtet ist.
Nur für Experten: Diese vereinfachte Darstellung ist für die im Beispiel gewählte Ladungsverteilung korrekt und sehr anschaulich. Gerade nach diesem Kriterium wurde das Beispiel gewählt. Allgemein ergibt sich das Dipolmoment aus dem Volumenintegral über das Produkt aus ortsabhängiger Ladungsdichte und Ortskoordinate. Wenn das Integral über die Ladungsdichte (die Gesamtladung) verschwindet, dann ist die "Ladungswolke" elektrisch neutral. In diesem Fall, der gerade dem Fall "normaler" (nicht ionisoisierter) Moleküle entspricht, ist die Definiton des Dipolmoments unabhängig vom Koordinatensystem und damit allgemeingültig.
 |
Die Fähigkeit des Wassers zur Wechselwirkung mit elektrischen Feldern lässt sich also durch dessen Dipomoment beschreiben. Es charakterisiert den Betrag und den Abstand der Ladung. Vorhandene äußere Felder greifen an diesen Ladungen an und richten den Dipol in Feldrichtung aus. |
 |
Das Wassermolekül lässt sich aber nicht als starrer Körper abstrahieren, vielmehr befinden sich die Atome des Moleküls jeweils im (Energie-) Minimum des (Wechselwirkungs-) Potentials gegenüber ihrem Nachbaratomen. "Mechanisch" kann das neben dem abstandsabhängigen Dipolmoment durch eine Feder zwischen den Ladungen beschreiben. |
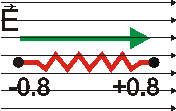 |
Bringt man nun das Wassermolekül in ein statisches elektrisches Feld, so folgt zweierlei: 1. Das Molekül (der Dipol) dreht sich, es richtet sich längs des Felds aus. 2. Die Ladungen erfahren eine statische Kraft, die zur Vergrößerung des Abstands (Dehnung der Feder, hier stark übertrieben dargestellt) führt. Dieser Fall entspräche etwa einem wassergefüllten Kondensator, in dem das als Dielektrikum wirkende Wasser ausgerichtet (polarisiert) wird. |
Für die IR-Spektroskopie interessiert aber die Wechselwirkung mit der elektrischen Komponente des elektromagnetischen (optischen) Wechselfelds:
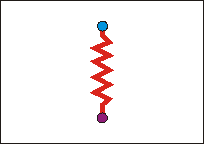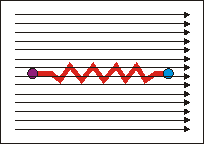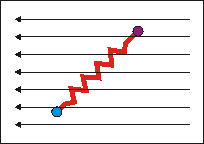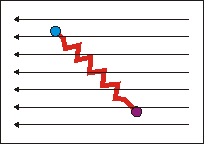 |
Wirkt ein solches elektrisches (oder optisches, d.h. elektromagnetisches) Feld auf den "federverbundenen Dipol" des Wassers ein, so beginnt dieser 1. zu rotieren und 2. in sich (in der Bindungslänge) zu schwingen. Das Molekül nimmt Rotations- und Schwingungsenergie auf, die dem anregenden elektromagnetischen Feld entstammt. |
Aus der Quantenmechanik ergibt sich, dass nur diskrete Energien erlaubt sind und Energiebeträge nur diskret aufgenommen werden können. Die Aufnahme von Energie ist deshalb nur genau dann möglich, wenn die Frequenz (Umpolen des el. Felds) der anregenden Strahlung mit der Übergangsfrequenz der Rotation bzw. Schwingung korreliert. Für reine Rotationsanregungen liegen diese Frequenzen im Mikrowellenbereich, in dem nicht genügend Energie zur Anregung der Schwingungen zur Verfügung steht. Die Schwingungsanregungen absorbieren im infraroten Spektralbereich. Da hier neben der Schwingungsanregung gleichzeitig und gemeinsam die niederenergetischeren Rotationen angeregt werden, entsteht ein Spektrum, dass aus mehreren Banden besteht, ein Rotations-Schwingungs-Spektrum.
Die reine Schwingungsbande A (ohne Rotationsanregung) kann nicht beobachtet werden, da nach quantenmechanischen Auswahlregeln gleichzeitig die Rotation angeregt werden muss. Entsprechend wird ein kleiner zusätzlicher Energiebetrag benötigt, die Bande verschiebt sich etwas zu höheren Energien B (zu höheren Wellenzahlen). Im Fall, dass das Molekül vor der Absorption bereits rotiert, kann auch gleichzeitig zur Schwingungsanregung die Rotation abgeregt werden. Der aus der Rotationsabregung zur Verfügung stehende Energiebetrag vermindert die zur Schwingungsanregung erforderliche Energie etwas, die Absorptionsbande verschiebt sich zu niedrigeren Wellenzahlen C.
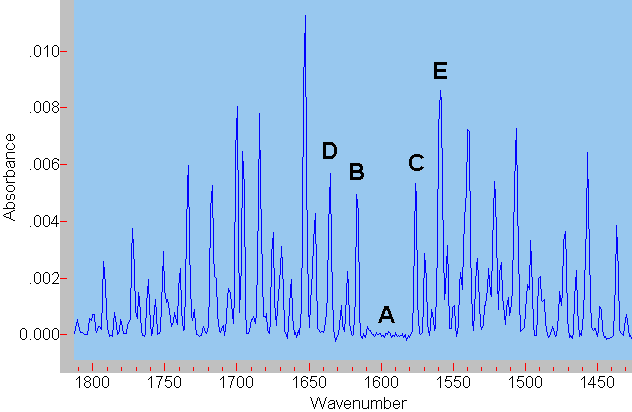
Daneben können noch Rotationen höherer Ordnung an- oder abgeregt werden. Dieser Sachverhalt lässt sich leider nicht aus dem hier präsentierten "mechanisch plausiblen" Modell erschließen. Er ergibt sich aus quantenmechanischen Berechnungen. Wird z. B. bei einer Schwingungsanregung gleichzeitig ein zweifacher Rotationsübergang angeregt, so ist hierfür natürlich noch etwas mehr Energie erforderlich, die Bande D erscheint noch weiter zu höheren Wellenzahlen verschoben. Analoges gilt bei Rotationsabregung, es entsteht Bande E.
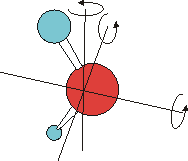 |
Wasser besitzt drei verschiedene, voneinander unabhängige Drehachsen. Die Rotation um jede dieser Drehachsen besitzt ein eigenes Trägheitsmoment. Deshalb benötigt die Anregung dieser verschiedenen Rotationen jeweils einen bestimmten, verschiedenen Energiebetrag. Korrespondierend ergeben sich jeweils drei Rotationsschwingungsbanden. Im Fall der Anregung der Schwingung gemeinsam mit einer Rotationsanregung sind das die Bande B und die beiden zwischen B und D gelegenen Banden. In allen anderen Fällen gilt diese Überlegung analog. |
Einige Nachbemerkungen:
1. Rotations-Schwingungs-Spektren lassen sich natürlich nur beobachten, wenn die Moleküle frei rotieren können. Das ist in der Gasphase der Fall. In Flüssigkeiten und Festkörpern werden die Rotationen unterdrückt.
2. Das hier präsentierte Modell veranschaulicht in vielen Fällen die Spektrenentstehung. Es gilt leider nur qualitativ. Gleichzeitig werden - wie in jedem Modell - einige Sachverhalte vereinfacht und andere ignoriert. Beispielsweise ignoriert dieses Modell komplett die Problematik der Auswahlregeln für die einzelnen Anregungen.
3. Exakte Berechnungen sind nur quantenmechanisch möglich.
4. Insider unter den Lesern entschuldigen bitte die starken Vereinfachungen des Modells. Häufig sind gerade diese modellhaften Vereinfachungen Basis für ein tieferes Verständnis auch weitergehender Probleme.
Moleküle, die einen Dipolmoment besitzen lassen sich - wie oben gezeigt - per IR-Stahlung zu Schwingungen anregen. Voraussetzung für die Möglichkeit der IR-Anregung eines Schwingungsübergangs (Anregung in einen anderen Schwingungszustand) in einem Molekül ist aber nicht unbedingt das anfängliche Vorhandensein eines Dipolmoments. Es reicht völlig, wenn sich durch die Schwingungsanregung das Dipolmoment ändert. Beim Wasser ist bereits ein Dipolmoment vorhanden, das sich durch die Schwingungsanregung ändert.

Beim Kohlendioxid hingegen ist kein anfängliches Dipolmoment vorhanden. Zwar sind die beiden Sauerstoffatome partial negativ und das Kohlenstoffatom partial positiv. Da aber das Molekül symmetrisch ist, heben sich die Polaritäten auf. Es kann jedoch mit infrarotem Licht zur z. B. asymetrischen Streckschwingung angeregt werden. Diese besitzt kein statisches, wohl aber der Bewegung entsprechend ein dynamisches Dipolmoment. Eine weitere im Kohlendioxid anregbare Schwingung ist die Deformationsschwingung (Schwingung im O-C-O Winkel)
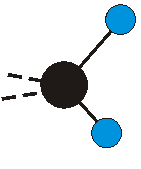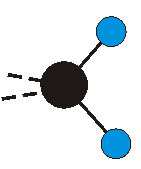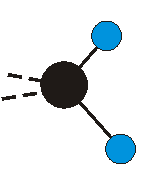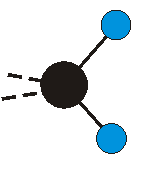
Voraussetzung für die IR-Anregung eines Schwingungsübergangs ist, dass sich das dynamische Dipolmoment während der Anregung ändert. Dies sei anhand zweier Schwingungen der Methylengruppe und einer Schwingung der Methylgruppe dargestellt:
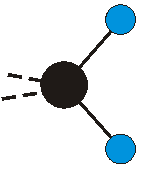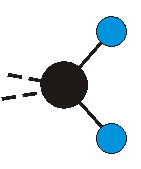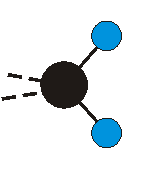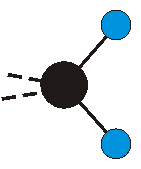 |
 |
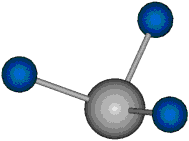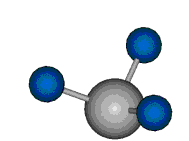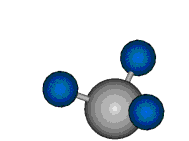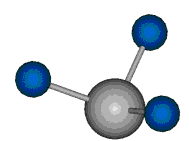 |
Die symmetrische Schwingung der Methylengruppe besitzt ein Dipolmoment, das auf der winkelhalbierenden Gerade des HCH-Winkels liegt. Würde sich die Methylengruppe komplett in Ruhe befinden, so wäre dieses Dipolmoment statisch vorhanden und würde sich nicht ändern. Es würde "dynamisch" ruhen. Schwingen nun beide H-Moleküle synchron in der Bindungslänge, so ändert sich während der Schwingung das Dipolmoment (in Bild unten links, rot dargestellt) ständig. Dieses veränderliche Dipolmoment lässt sich auch ausdrücken als ein mittleres Dipolmoment (nicht dargestellt) und der Abweichung (blau dargestellt) des Dipolmoments von seinem Mittelwert.
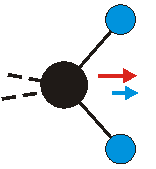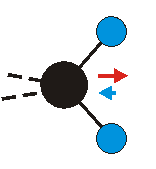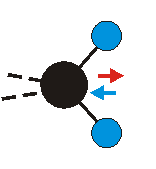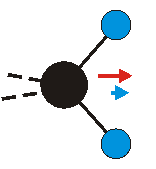 |
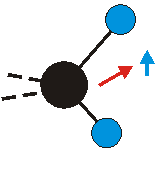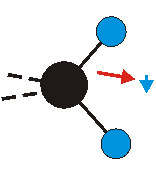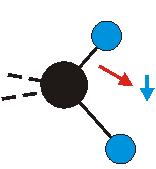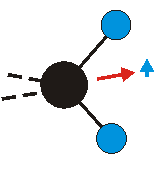 |
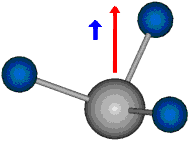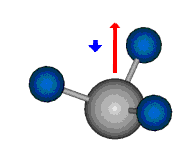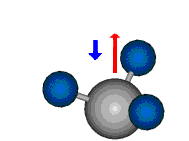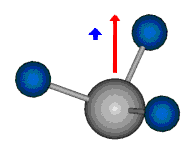 |
Bei der asymmetrischen Methylenstreckschwingung ändert sich das Dipolmoment in der Richtung, der Betrag bleibt annähernd konstant. Der Mittelwert des Dipolmoments liegt wiederum auf der Winkelhalbierenden des HCH-Winkels, die Richtung des mittleren Dipolmoments ist mit der der symmetrischen Streckschwingung identisch. Als dynamisches Dipolmoment ergibt sich jedoch der Differenzvektor des momentanen Dipolmoments zum Mittelwert. Das dynamische Dipolmoment liegt deshalb in der HH-Verbindungslinie. Bei der symmetrischen CH3-Schwingung sind - wie dargestellt - das Dipolmoment als auch das dynamische Dipolmoment - in der Raumdiagonale des C-HHH-Winkels, also in Richtung der letzten CC-Bindung einer Alkylkette gerichtet.
Zusammenfassung: Die Abweichung - das dynamische Dipolmoment - muss sich während einer Schwingungsanregung ändern. Nur so lassen sich Schwingungsübergänge mit Hilfe von IR-Licht anregen. Zu beachten ist, dass ein dynamisches Dipolmoment vor der Schwingungsanregung vorhanden sein kann, aber nicht muss. Es ist auch ausreichend, wenn durch die Anregung ein Dipolmoment entsteht.
Schwingungen betreffen streng genommen immer ein Molekül als Ganzes. In guter Näherung lassen sich jedoch viele Schwingungen eines Moleküls isoliert betrachten. Im Methylen-Beispiel oben bewegt sich das Kohlenstoffatom nicht, was streng genommen nicht korrekt, sondern nur Näherung ist. Die Methylengruppe schwingt genau so, dass der Schwerpunkt aller drei Atome in Ruhe bleibt, d. h. bewegen sich die beiden H-Atome auf das C zu, so bewegt sich auch das C ein wenig auf die H zu. Da die H-Atome aber wesentlich leichter sind als die C-Atome sind, bewegt sich das C-Atom viel weniger. Es befindet sich annähernd in Ruhe.
Die Schwingungsamplitude der einzelnen Moleküle ist indirekt proportional zu ihrer Masse. Schwere Atome schwingen schwächer als leichte. Gleichzeitig schwingen schwere Atome langsamer als leichte, was in der Massenträgheit begründet liegt. Die Frequenz der Schwingungen in beispielsweise einer Alkankette lassen sich so in verschiedene Bereiche unterteilen: Die H-Atome der einzelnen Methylengruppe schwingen viel schneller als die Methylengruppen gegeneinander (Deformationsschwingungen im C-C-C Winkel). Man kann diese verschiedenen Schwingungen in Näherung einzeln betrachten. Die Abstraktion auf einzelne Molekülgruppen führt zum Konzept der Gruppenfrequenzen.
Vielen funktionelle Gruppen besitzen charakteristische Absorptionsfrequenzen bzw. -wellenzahlen. Diese sind annähernd konstant und nur wenig von ihrer chemischen Umgebung im Molekül abhängig. Gleichwohl - und das ist die Näherung - verschieben (Shift) sie in deren Abhängigkeit um einen geringen Wert. So liegt beispielsweise die Absorption der C=O Doppelbindung einer Carbonylgruppe (-COOH) bei 1705 cm-1, wobei sie je nach Umgebung im Bereich 1680...1760 cm-1 liegen kann.
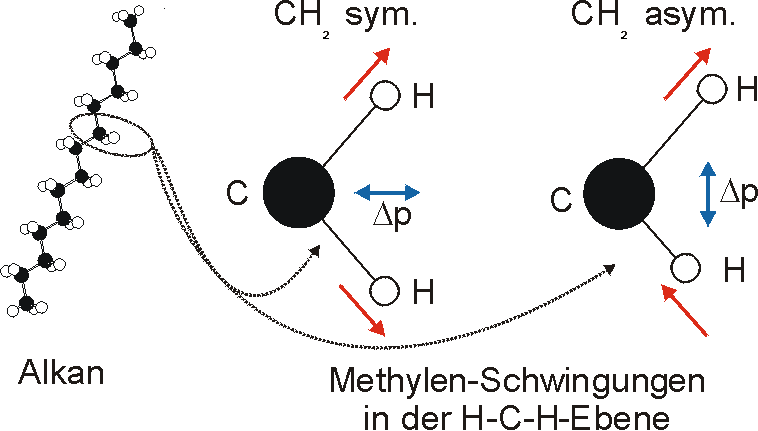
Innerhalb der einzelnen Schwingungsgruppen lassen sich die einzelnen Absorptionsbanden bestimmten Schwingungsübergängen zuordnen. In einem Alkan gibt es die Methylengruppen, die z.B. symmetrische und asymmetrische Streckschwingungen beschreiben. Entsprechend ordnen sich die dynamischen Dipolmomente (im Bild blau) zu.
Weitere Schwingungen der CH2-Gruppe sind:
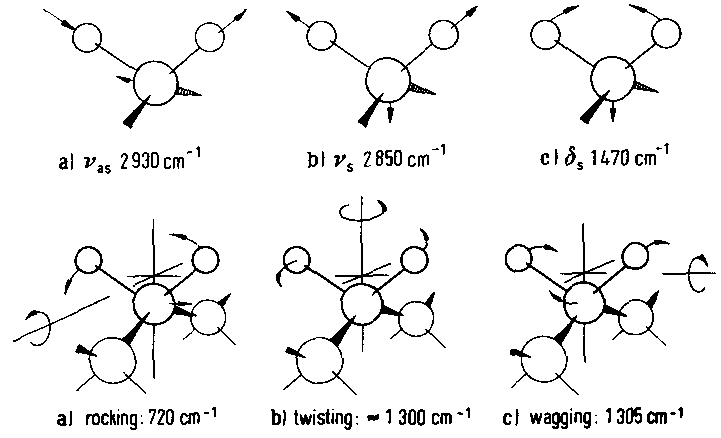
Anhand der über den Index erreichbaren IRRAS-Methode lassen sich die Dipolmomente einzeln quantitativ messen und sich daraus die Anordnung der Moleküle auf Oberflächen bestimmen.
In der IR-Literatur ist die Bezeichnung der einzelnen Schwingungen mit Symbolen üblich. Einzelne Schwingungsbezeichnungen wurden im Text bereits bekannt gemacht. Nachfolgend erscheint eine Tabelle mit den Bezeichnungen der wichtigsten Molekülschwingungen.
| Symbol | Bezeichnung der Schwingungsform | |
| a, b | i. p. Deformationsschwingung, allgemein | |
| G | o. o. p. Deformationsschwingung von Gerüstatomen | |
| g | o. o. p. Deformationsschwingung | |
| D | i. p. Deformationsschwingung von Gerüstatomen | |
| d | i. p. Deformationsschwingung einer X-H-Bindung | |
| ds | symmetrische Deformationsschwingung (bending) | |
| das | asymmetrische Deformationsschwingung (bending) | |
| d' | Deformationsschwingung (twisting, rocking) | |
| k | o. o. p. wagging Schwingung einer XH2-Gruppe (X ¹ C) | |
| r | rocking Schwingung | |
| rb | i. p. rocking Schwingung | |
| rg | o. o. p. rocking Schwingung | |
| r | i. p. rocking Schwingung einer XH2-Gruppe (X ¹ C) | |
| n | Streckschwingung einer X-H-Bindung | |
| ns | symmetrische Streckschwingung | |
| nas | asymmetrische Streckschwingung | |
| nb | i. p. Streckschwingung | |
| ng | o. o. p. Streckschwingung | |
| t | twisting Schwingung | |
| t | Torsion, twisting Schwingung einer XH2-Gruppe (X ¹ C) | |
| F | o. o. p. Ring-Deformationsschwingung | |
| w | wagging Schwingung | |
| w | Streckschwingung von Gerüstatomen ohne H-Bindung |
| Fragen, Hinweise, Kritiken: |