Beim Durchgang durch ausgedehnte Medien wird die Energie einer elektromagnetischen Welle spektral selektiv absorbiert. Betrachten wir diese Absorption für eine konstante Wellenlänge an einem Absorptionsmaximum. Innerhalb der differentiellen Schichtdicke dr wird die einfallende Strahlungsintensität I um den gleichen Bruchteil geschwächt:
| (1.1) |
Der Absorptionskoeffizient a ist eine Stoffkonstante und hat die Dimension 1/Länge. Durch Integration folgt aus Gleichung 1.1 das Beersche Gesetz
| (1.2) |
Handelt es sich um gelöste Stoffe in einem praktisch durchsichtigen Lösungsmittel oder wie in der IR-Spektroskopie häufig um pulverisierte Substanzen in oberhalb von 400 cm-' transparentem KBr, so ist der Absorptionskoeffizient proportional zur Konzentration:
| (1.3) |
wobei c die Konzentration in g/l, mol/l o. ä. ist. e heißt entsprechend der g/l- bzw. molare Extinktionskoeffizient. Gleichung 1.3 eingesetzt in 1.2 ergibt das Lambert-Beer-Gesetz
| (1.4) |
Die durch Herleitung aus den Maxwellgleichungen für das elektrische Feld E gewonnene Wellengleichung
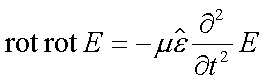 |
(2.1) |
besitzt als Lösung die Gleichung einer Welle
| (2.2) |
wobei w = pn (n...Frequenz) die Kreisfrequenz, t die Zeit, kM der Betrag des Wellenvektors (k = 2pn/l) im umgebenden Medium und r der Weg der sich ausbreitenden Welle ist. In absorbtionsfreien Medien nutzt man den ("normalen") Brechungsindex n zur Beschreibung des optischen Verhaltens des Mediums. Er verbindet die Beträge der Wellenvektoren
| (2.3) |
im Medium und im Vakuum miteinander. Durch Einsetzen in Gl. 2.2 ergibt sich
| (2.4) |
In absorbierenden Medien nutzt man den komplexen Brechungsindex
| (2.5) |
zur Beschreibung der optischen Materialeigenschaften. Der Realteil n entspricht der in Gl. 2.3 genutzten Brechzahl und beschreibt die Dispersion im Medium. Der komplexe Anteil k (nicht zu verwechseln mit dem Wellenvektor kM, V) beschreibt die Absorption im Medium, was nachfolgend gezeigt wird. Nach Einsetzten von Gl. 2.5 in Gl. 2.4 folgt
| (2.6) |
Durch Aufspaltung des Exponenten einzelne Faktoren ergibt sich
| (2.7) |
und mit i2=-1
| (2.8) |
Der schwarze Term beschreibt die Zeitabhängigkeit der Welle, der blaue deren Ortsabhängigkeit. Beide Terme entsprechen der für absorptionsfreie Ausbreitung bekannten Welle (Gl. 2.4). Der rote Term beschreibt die Dämpfung der Welle während der Ausbreitung.
Die Frequenzen der Wellen im Infraroten liegen im Bereich 1015 Hz. Infrarotdetektoren besitzen Zeitkonstanten unter 106 Hz. Sie mitteln deshalb über mehrere Millionen Schwingungen. Die gemessene Intensität ist deshalb
| (2.9) |
Die ersten beiden Terme vom Gl. 2.8 beschreiben Sinus-Funktionen, die sich zu Null mitteln. Nur der letzte Term liefert eine Beitrag
| (2.10) |
Der Vergleich mit dem Lambert-Beerschen Gesetz zeigt eine übereinstimmende Struktur und manifestiert theoretisch die Korrektheit des experimentell gefundenen Gesetzes, wobei lediglich die Stoffkonstanten umdefiniert werden müssen.
Die Intensität definiert sich optisch als Energie W pro Zeit t und Fläche A
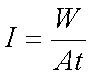 |
(3.1) |
und unter Nutzung des Weg/Zeit-Gesetzes
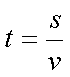 |
(3.2) |
(s...Weg, v...Geschwindigkeit). Entsprechend ergibt sich mit dem Volumen V = As
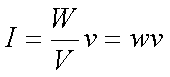 |
(3.3) |
mit w als zeitlich gemittelter Energiedichte und v als Ausbreitungsgeschwindigkeit der Welle. Nach Einsetzten der Energiedichte-Feldstärke-Beziehung für elektromagnetische Felder
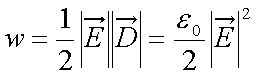 |
(3.4) |
in Gl. 3.3 ergibt sich die Bezeihung zwischen der Intensität und dem elektrischem Feld einer Welle
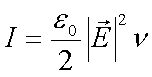 mit e0 = 8.854·10-12 C2 / Nm2 und v = cL/n mit e0 = 8.854·10-12 C2 / Nm2 und v = cL/n |
(3.5) |
Durch Einsetzen für I und I0 in das Lamber-Beersche Gesetz (Gl. 1.4, für das Innere eines homogenen Mediums mit dem Brechungsindex ![]() =n + ik ) und kürzen der beidseitig gleichen Faktoren folgt das Lamber-Beersche Gesetz mit Bezug auf die Feldstärke E der optischen Welle
=n + ik ) und kürzen der beidseitig gleichen Faktoren folgt das Lamber-Beersche Gesetz mit Bezug auf die Feldstärke E der optischen Welle
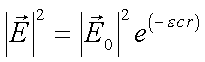 |
(3.6) |
Andererseits ergibt sich die Ortsabhängigkeit des elektrischen Feldvektors ![]() aus der Lösung der Wellengleichung
aus der Lösung der Wellengleichung
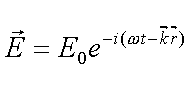 mit mit 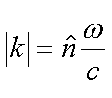 und und 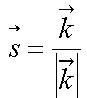 |
(3.7) |
(![]() ...Wellenvektor,
...Wellenvektor,![]() ...Poyntingeinheitsvektor (Einheitsvektor in Ausbreitungsrichtung)) als
...Poyntingeinheitsvektor (Einheitsvektor in Ausbreitungsrichtung)) als
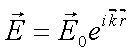 |
|
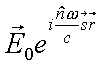 |
|
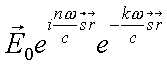 |
(3.8) |
(k ist hier Imaginärteil von ![]() ).
).
Da nur der zweite Exponentialterm von Gl. 3.8 das zeitliche Mittel der Feldstärke ändert, kann man Gleichung 3.8 schreiben als
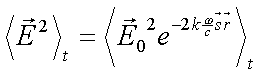 |
|
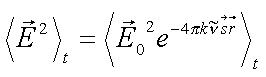 mit mit 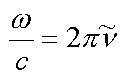 |
(3.9) |
(![]() ...Wellenzahl) oder
...Wellenzahl) oder
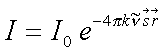 |
(3.10) |
Dieser Ausdruck muß gleich dem Lambert-Beer-Gesetz (Gl. 1.4) sein, so daß sich der Imaginärteil k des Brechungsindex über den Absorptionskoeffizienten bestimmen läßt:
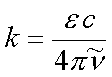 |
(3.11) |
Direkt bezogen auf die Extinktion (Absorbance) A´ = ln (I0 / I) ergibt sich
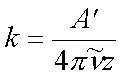 |
(3.12) |
wobei z = s·r die absorbierende Schichtdicke in Ausbeitungsrichtung der Welle ist. Unter Verwendung des Umrechungsfaktors ln10 = 2.30 zwischen der bisher verwendeten natürlichen und der experimentell über den dekadischen Logarithmus definierten "spektroskopischen" Extinktion A ergibt sich der Imaginäranteil k des Brechungsindex mit
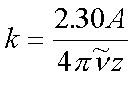 |
(3.13) |
Mikroskopisch steht Absorption für die Wahrscheinlichkeit P, daß ein Molekül mit dem elektrischen Feld Energie austauscht und vom Schwingungsgrundzustand in den ersten angeregten Zustand wechselt. Diese ist gleich dem Produkt von Einstein-Koffizient 8p3/3h2, dem Quadrat des Übergangsmatrix-Elementes ![]() , der Strahlungsdichte r mit passender Energie hn und dem Besetzungszahlunterschied N1-N0 zwischen beiden Niveaus:
, der Strahlungsdichte r mit passender Energie hn und dem Besetzungszahlunterschied N1-N0 zwischen beiden Niveaus:
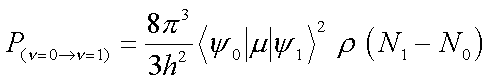 |
(4.1) |
Der durch Absorption verursachte Intensitätsverlust dI innerhalb einer Schichtdicke dz ist gleich dem Produkt aus Anregungswahrscheinlichkeit P, Anregungsenergie hv und dz.
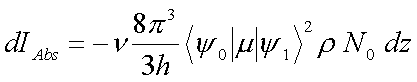 |
(4.2) |
Teilweise kompensiert wird der Verlust durch Absorption von einer induzierten Emission, die proportional zur Zahl der Moleküle im angeregten Zustand ist:
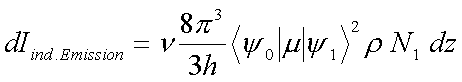 |
(4.3) |
Im thermischen Gleichgewicht beträgt das Verhätnis der Anzahl schwingungsangeregter Moleküle zur Anzahl der Molekükle im Grundzustand exp![]() (
(![]() ... Wellenzahl). Deshalb ist die induzierte Emission um diesen Faktor kleiner als die Absorption. Für Schwingungsanregungen mit mehr als 1000 cm-1 Energiedifferenz kann man daher bei Raumtemperatur (Þ
N0/N1=120) den Beitrag der induzierten Emission vernachlässigen:
... Wellenzahl). Deshalb ist die induzierte Emission um diesen Faktor kleiner als die Absorption. Für Schwingungsanregungen mit mehr als 1000 cm-1 Energiedifferenz kann man daher bei Raumtemperatur (Þ
N0/N1=120) den Beitrag der induzierten Emission vernachlässigen:
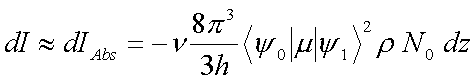 |
(4.4) |
Die Strahlungsdichte r läßt sich ersetzen durch I / c (c...Lichtgeschwindigkeit), so daß Gleichung 4.4 umgeschrieben werden kann zu
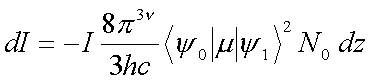 |
(4.5) |
Das Matrixelement des zur i-ten Absorptionsbande (Normalmode) gehörenden Dipolmomentes
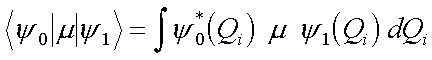 |
(4.6) |
kann durch Taylor-Reihen-Entwicklung in Normalkoordinaten Qi
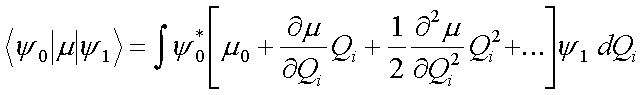 |
(4.7) |
und Abbruch nach dem linearen Term vereinfacht dargestellt werden als
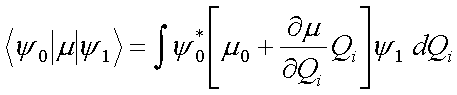 |
|
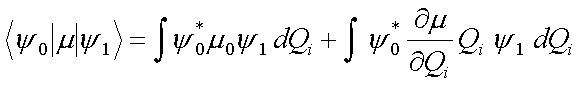 |
(4.8) |
In der Näherung des harmonischen Oszillators gilt µ0 = const (Gleichgewichtsabstand unverändert). Im ersten Summanden laßt sich µ0 aus dem Integral herausziehen. Das verbleibende Intergal verschwindet, da es sich um ein Integral über orthogonale Wellenfunktionen handelt. Es verbleibt
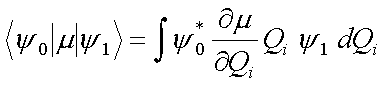 |
|
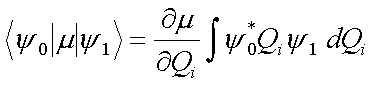 |
(4.9) |
Der Integral-Term in Gleichung 4.9 (die Änderung des Erwartungwertes für die Normalkoordinate Qi) läßt sich für einen harmonischen Oszillator mit der Eigenfrequenz v und einer Energiezunahme hv analytisch lösen:
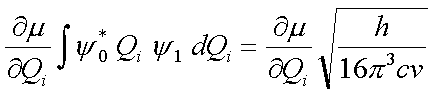 |
(4.10) |
Einsetzen in Gleichung 4.5 ergibt
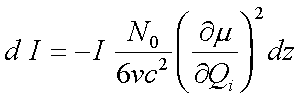 |
(4.11) |
und unter Berücksichtigung der vektoriellen Charaktere des die Intensität verursachenden elektromagnetischen Felds und des dynamischen Dipolübergangsmoments
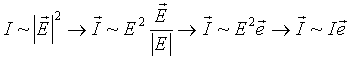 und und |
(4.12) |
mit ![]() als Einheitsvektor des elektrischen Felds folgt
als Einheitsvektor des elektrischen Felds folgt
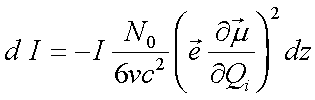 |
|
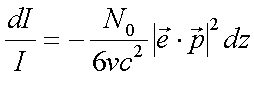 und und 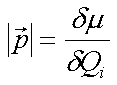 | (4.13) |
Integration führt zu
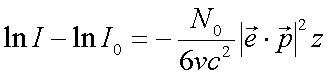 |
|
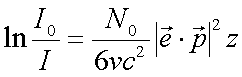 |
(4.14) |
Mit A´ = ln (I0 / I) beziehungsweise A´ = 2.30 lg (I0 / I) = 2.30 A folgt
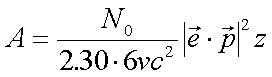 |
(4.15) |
Nach Einsetzten in Gleichung 3.13 ergibt sich
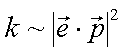 |
(4.16) |
Gleichung 4.16 ist die Grundlage aller Methoden zur Bestimmung der mittleren Orientierung von Molekülen durch IR-Spektroskopie: Die Abnahme der IR-Strahlungsintensität ist proportional zum Betragsquadrat des Vektorproduktes von elektrischem Feld ![]() und einem Vektor , dem sogenannten dynamischen Dipolmoment
und einem Vektor , dem sogenannten dynamischen Dipolmoment![]() , synonym Dipolübergangsmoment oder Übergangsdipolmoment (engl. TDM = transition dipol moment), welches parallel zur entsprechenden Normalkoordinate Qi (Verschiebung des Ladungsschwerpunkts bei Ausführung der Schwingung einer Normalmode) orientiert ist.
, synonym Dipolübergangsmoment oder Übergangsdipolmoment (engl. TDM = transition dipol moment), welches parallel zur entsprechenden Normalkoordinate Qi (Verschiebung des Ladungsschwerpunkts bei Ausführung der Schwingung einer Normalmode) orientiert ist.
Der komplexe Brechungsindex k kann durch Messung der Extinktion aus dem Spektrum eines KBr-Presslings gewonnen werden. Solche Spektren werden auch Volumenspektren genannt. Dazu wird eine bekannte Menge KBr mit einer bekannten Menge der zu untersuchenden Substanz gemeinsam gemörsert und anschließend zu einer Tablette verpreßt. Diese Tablette wird gewogen und aus dem Verhältnis KBr-Einwaage zu Tablettenmasse die Substanzeinwaage bzw. Konzentration bestimmet.
Absorptionsspektrum ( A = lg (I0 /I) ) und Imaginärteil k des Brechungsindex eines Preßlings hängen nach Gl. 3.13 zusammen zu:
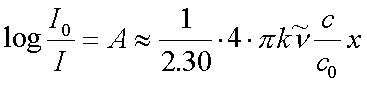 |
(5.1) |
Dabei steht x für die Dicke des Preßlings und der Faktor c/c0 für deren Substanz-Konzentration relativ zur reinen Substanz. Alternativ (einfacher) kann man sich den Preßling als entmischt vorstellen. Dann besteht der Preßling aus einer dünnen Schicht Substanz und einer dickeren Schickt KBr. Die KBr-Schicht absorbiert per Voraussetzung im interessierenden Spektralbereich nicht. Die effektive Schichtdicke xeff der Substanz läßt sich dann aus der Masse der Substanz-Einwaage, deren Dichte und dem Durchmesser des Preßlings (meist 13mm) berechnen. Gleichung 4.1 vereinfacht sich zu
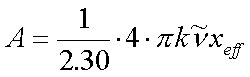 |
(5.2) |
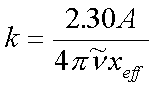 |
A...Extintion (Peakfläche) xeff...effektive Schichtdicke der Einwaage |
(5.3) |
Das so gewonnene k-Spektrum gilt nur in isotropen Substanzen. Bemerkungen zur Anisotropie von Substanzen finden sich in den IRRAS-Grundlagen
|
|
Fragen, Hinweise, Kritiken:
|