IRRAS heißt Infrarot-Reflexions-Absorptions-Spektroskopie. Als synonyme Bezeichnungen sind ERAS (External Reflection Absorption Spectroscopy) oder ERS (External Reflection Spectroscopy) gebräuchlich. Bei dieser Meßmethode wird IR-Licht an der Aussenseite einer Metall-Oberfläche (extern) reflektiert. Ziel ist die Spektroskopie von sich auf dieser Oberläche befindlichen, dünnen Schichten. Die Empfindlichkeit dieser Meßmethode reicht aus, um IR-Spektren selbst monomolekular dünner Filme mit einer Schichtdicke von einigen Ångström messen zu können. Typische Bandenhöhen dieser Monolayer liegen im Bereich unterhalb 0,005 AU (Absorbance Units). Als Beispiel ist nachfolgend das Spektrum von Oktadeklanthiol auf Gold(111) dargestellt.
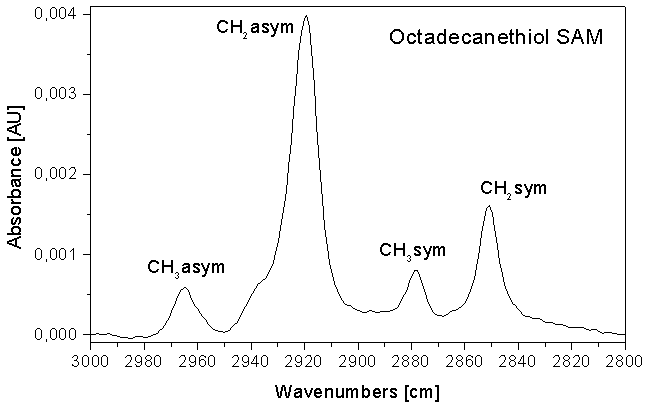
Monolayer können als Langmuir-Blodgett-Filme oder als selbstordnende Filme (SAM = self assembled monolayer) ausgebildet wedren. SAMs auf Oberflächen bilden kristallin geordnete Strukturen aus. Dabei ordnen sich die Moleküle aus ihrer Struktur und aus der Oberflächenstruktur heraus im Resultat des Selbstordnungsprozesses so, daß eine Energieminimierung im SAM eintritt. Im Resultat beitzen alle Moleküle einen einheitlichen Verkippungswinkel gegen die Oberflächennormale (Bild unten)

Wegen der hohen Sensitivität der Meßmethode liegt neben der chemischen Analytik der Filme ein Hauptanwendungsgebiet der IRRAS-Methode in der Bestimmung der Orientierung der SAMs. Diese Orientierungsbestimmung ist der Gegenstand der nachfolgenden Betrachtung.
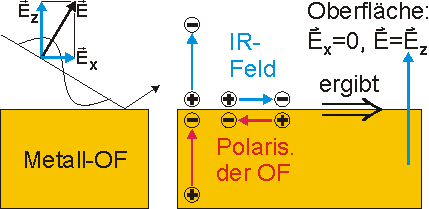
Der elektrische Anteil (E-Feld) des auf die Oberfläche einfallenden IR-Lichts (elektromagnetische Welle) wechselwirkt mit in der Oberfläche vorhandenen Ladungen. Das Besondere an Metallen ist dabei, daß diese aus frei beweglichen, negativ geladenen Elektronen und im Metallgitter fixierten, positiv geladenen Atomrümpfen bestehen. Die Wechselwirkung erfolgt mit den Atomrümpfen als auch mit den Elektronen. Natürlich führt die Wechselwirkung mit den positiven Atomrümpfen nicht zu einer merklichen Polarisation, da diese nahezu ortsfest im Kristallgitter des Metalls fixiert sind. Die innerhalb des Metalls frei beweglichen Elektronen hingegen werden durch die elektrische Kraft des von aussen einwirkenden E-Felds verschoben. Das Metall wird an der Oberfläche polarisiert.
Das im Bild oben links dargestellte, von aussen einwirkende E-Feld der Welle wird an der Oberfläche in Komponenten senkrecht und parallel zur Oberfläche aufgespalten. Die parallel zur Oberfläche gerichtete Komponente verursacht eine Verschiebung von Elektronen parallel zur Oberfläche. Es entsteht eine Anhäufung negativer geladener Elektronen und positiv geladener Atomrümpfe (eine Polarisation) in Folge derer sich ein elektrisches Feld an der Metalloberfläche aufbaut. Es ist der Ursache - dem äußeren Feld - entgegengesetzt gerichtet. Die Ladungsverschiebung erfolgt genau so lange, bis das äußere und das durch Polarisation erzeugte Feld gleich stark sind. Dann addieren sich beide Felder zu Null, sie heben sich auf. Damit entfällt die ursächlich wirkende, elektrische Kraft, es werden keine weiteren Polarisationsladungen aufgebaut. Die senkrecht der Oberfläche gerichtete Feldkomponente erzeugt ein Polarisationsfeld, daß dem äußeren Feld gleichgerichtet ist und sich zu diesem addiert. Es kommt zu einer Verstärkung der Normalkomponente des einfallenden Felds.
Der ganze Vorgang findet ständig (dynamisch) statt, da das von außen einwirkende E-Feld von einer Welle herrührt, deren Polarität und Feldstärke sich mit ihrer Frequenz ständig ändert. Im infraroten Spektralbereich ist die Trägheit der Elektronen vernachlässigbar. Die Elektronen können auf Änderung des äußeren E-Felds unmittelbar reagieren. Die Feldkompensation erfolgt vollständig. Hingegen spielt die Trägkeit der Elektronen im Ultravioletten eine zunehmende Rolle. In Bereichen weicher Röntgenstrahlen und kurzwelliger ändert sich das E-Feld so schnell, daß die Elektronen wegen ihrer Trägheit dem E-Feld nicht mehr folgen können. Dann entfällt die Oberflächenauswahlregel vollständig. Die "Grenze" (eigentlich ein kontinuierlicher Übergang) zwischen beiden Bereichen entspricht der Plasmafrequenz des "Elektronengases" im konkreten Metall und liegt meist in tiefen UV (100..200 nm).
Zur Ausführung von IRRAS-Messungen bedient man sich deshalb des folgenden Versuchsaufbaus:
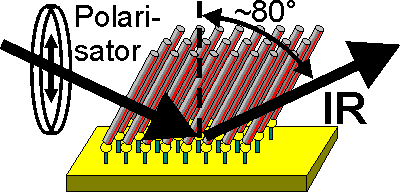
Die Messungen erfolgen mit p-polarisiertem Licht, da s-polarisierte Anteile des E-Felds nicht zur Messung beitragen können. Sie würden nur zusätzlichen "Energieballast" am Detektor erzeugen und das Rauschen erhöhen. Der Einfallswinkel wird so gewählt, das möglichst viele Anteile des einfallenden p-polarisierten E-Felds senkrecht zur Oberfläche stehen. Deshalb empfielt sich ein möglichst streifender Einfall. Andererseits erhöht der flacher werdende Einfallswinkel die zur Reflexion erforderliche Probenoberfläche. Bei begrentzter Oberfläche führt das zu Energieverlusten und zur Erhöhung des Streulichts im Probenraum. Deshalb wird als Kompromiß ein Einfallswinkel von etwa 80° empfohlen. Optimale Werte werden im Versuch ermittelt.
Dipolmomente, genauer gesagt dynamische Dipolmomente oder auch Dipolübergangsmomente (engl. TDM = Transition Dipol Momentum), sind die Grundlage der Wechselwirkung elektromagnetischer Strahlung mit Atomen und Molekülen. Grundlegende Ausführungen finden sich im einleitenden Kapitel dieser Seiten. Diese Aussage trifft neben Molekülschwingungsübergängen, wie hier dargestellt, auch allgemein auf andere elektromagnetisch angeregte Übergänge zu. Weitere Beispiele sind die elektronischen Übergänge in Atomem und Molekülen.
Die Extinktion hängt mit dem Dipolübergangsmoment ursächlich zusammen. Sie ergibt sich aus dem Übergangsdipolmoment, wobei Teilchenzahlen und Besetzungszahlen anzuregender Übergänge als Proportionalitätsfaktoren eingehen. Wichtig zu erwähnen ist an dieser Stelle der vektorielle Charackter des Dipolübergangsmoments. Eine Anregung erfolgt nur, wenn das einfallende E-Feld dem Dipolübergangsmoment parallele Anteile besitzt. Stehen beide Vektoren senkrecht zueinander, kann keine Anregung erfolgen.
Übliche Spektrometer-Lichtquellen sind thermische Strahler. Deshalb wird beim Vermessen von Proben in Rahmen der "konventionellen" Analytik auch an isotropen Proben keine Richtungsabhängigkeit festgestellt.
Makroskopisch beschreibt man das Dipolübergangsmoment auch durch den Imaginärteil des komplexen Brechungsindex. Er ist unter Berücksichtigung der Konzentration und der Besetzungszahlen (meist verbachlässigbar) dem Übergangsdipolmoment proportional. Details sind in den weiterführenden Seiten zu lesen.
Im KBr-Pressling befinden sich kleine Kristallite der Substanz in einer statistisch gleichverteilten Orientierung, d. h. die Dipolmomente verteilen sich isotrop im Raum. Deshalb mißt man hier nur die Extinktionen, die der Projektion des E-Vektors auf alle Dipolübergangsmomente des gemessenen Übergangs entsprechen. Die Projektion erfolgt mit der Cosinus-Funktion des eingeschlossenen Winkels. Da die der Messung zugrunde liegenden Intensitäten dem Quadrat des E-Vektors entsprechen, skaliert die Extinktion natürlich mit dem Quadrat des Cosinus. Mathematisch betrachtet mißt man die Wechselwirkung zwischen dem E-Feld und dem über alle Raumrichtungen mit dem cos2-gemitteten Dipolübergangsmoment. Mittelt man einen Einheitsvektor derart, so ergibt sich 1/3 als Mittelwert. Deshalb erhält man als Extinktionsmeßwert nur 1/3 der maximal möglichen Wechselwirkung bei ideal paralleler Orientierung aller Dipolübergangsmomente zum E-Vektor. Anders herum kann man aber aus dem Extinktionsmesswert die Größe des Dipolübergangsmoments bestimmen, indem man den Meßwert einfach mit Drei multipliziert (und die Konzentration herausrechnet).
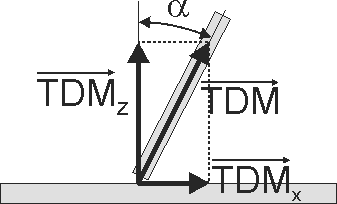
Betrachten wir nun die Orientierung einer schwingenden Gruppe eines Moleküls an der Metalloberfläche vereinfacht im zweisimendionalen Fall. Das Dipolübergangsmoment (TDM) soll im Beispiel längs der Molekülachse liegen. Dann spaltet sich das TDM in Komponenten parallel (TDMx) und normal (TDMz) zur Oberfläche auf. Der Betrag des TDM kann, wie oben beschrieben, durch Messungen am Pressling bestimmt werden. Die Richtung des TDM ist aus dem Molekülbau bekannt. Bei einer IRRAS-Messung wird die x-Komponente des E-Felds durch die Metalloberfläche unterdrückt, TDMx ist der Messung nicht zugänglich. Allein die Normalkomponente des TDM, TDMz, kann wechselwirken und wird gemessen. Durch Vergleich des mit Drei multiplizierten Pressling-Messwerts mit dem Oberflächenmesswert ergibt dann den cos2 des zwischen TDM und Oberflächennormale eingeschlossenen Winkels. Unter Kenntnis der Orientierung des TDM im Molekül kann daraus der Winkel der Molekülachse zur Oberfläche berechnet werden.
In der Praxis, die leider nicht nur zweidimensional ist, könnte man die restlichen Orientierungen (Drehung des Moleküls um seine Achse, Drehung des Moleküls um die Oberflächennormale) durch Berücksichtigung weiterer Schwingungsübergänge aus einem Gleichungssystem berechnen. Voraussetzung ist, daß die TDMs dieser Übergänge andere Richtungen besitzen und einen dreidimensionalen Raum aufspannen. Leider gibt es in der Praxis noch ein weiteres Problem: Der die Oberfläche bedeckende SAM erzeugt eine Reflexion an seiner äußeren Oberfläche. Diese Reflexion schwächt die Intensität der gemessenen Banden, da die reflektierten Lichtanteile nicht den Film durchdringen und somit nicht zur Extinktion beitragen. Im Allgemeinen läßt sich bei bekannter Brechzahldifferenz (ober- und unterhalb einer Grenzfläche) die Reflektivität der Grenzfläche aus den Fresnell'schen Formeln berechnen. Nur ist die Brechzahl (der Realteil des komplexen Brechungsindex) des Films in der Nähe der bei den Messungen interessierenden Absorptionsbanden nicht konstant. Dort verändert sich der Imaginärteil des komplexen Brechungsindex und führt zu anormaler Dispersion der Brechzahl. Real- und Imaginärteil den komplexen Brechungsindex sind über die Kramers-Kronig-Transformation miteinander verbunden und lassen sich auseinander berechnen. Zusammenfassend möchte man aus der Stärke der Bande im IRRAS-Spektrum die Orientierung des Moleküls bestimmen, die Orientierung des Moleküls beeinflußt aber die Stärke der Bande. Dieser Zirkelbezug läßt sich exakt nur durch die Methode der Orientierungsbestimmung nach Parikh und Allara (Absolutmethode) lösen, bei der das Oberflächenspektrum unter Variation der Orientierung exakt berechnet und mit dem Oberflächenspektrum evrglichen wird.
|
|
Fragen, Hinweise, Kritiken:
|