In diesem Beitrag soll die Bestimmung der Orientierung monomolekular dünner Filme auf Metalloberflächen beschrieben werden. Die Bestimmung erfolgt nach der Absolutmethode: Aus dem Volumenspektrum eines Presslings wird unter Vorgabe der Molekülorientierung auf der Oberfläche das k-Spektrum (komplexer Brechungsindex) normal zur Oberfläche bestimmt. Aus diesem kann das Spektrum der reellen Brechzahl durch Ausführung einer Kramers-Kronig-Transformation berechnet werden. Es folgt die Berechnung der die Messanordnung transmittierten Intensität durch Lösung der (optischen) Wellengleichung. Führt man diese Berechnungen für die unbeschichtete und die beschichtete Metalloberfläche aus, bildet den Quotienten und logarithmiert, dann erhält man das berechnete IRRAS-Spektrum. Es kann mit dem gemessenen vergleichen werden. Die Orientierung der Moleküle geht als Parameter in die Berechnung ein und wird solange verändert und die Berechung wiederholt, bis sich eine befreidigende Übereinstimmung von berechnetem und gemessenem IRRAS-Spektrum ergibt.
Im KBr-Pressling befinden sich kleine Kristallite der Substanz in einer statistisch gleichverteilten Orientierung, d. h. die Dipolmomente verteilen sich isotrop im Raum. Deshalb mißt man hier nur die Extinktionen, die der Übergangswahrscheinlichkeit P multipliziert mit der Projektion des Richtungsvektors p (Einheitsvektor) des Dipolübergangsmomentes des jeweiligen gemessenen Übergangs auf den E-Vektor des IR-Lichts entspricht. Die Projektion erfolgt, wie bei den Ausführungen zum TDM in Gl. 4.16 beschrieben, mit der Cosinus-Funktion des eingeschlossenen Winkels. Da die der Messung zugrunde liegenden Intensitäten dem Quadrat des E-Vektors entsprechen, skaliert die Extinktion natürlich mit dem Quadrat des Cosinus.
Mathematisch betrachtet mißt man die Wechselwirkung zwischen dem E-Feld und dem über alle Raumrichtungen (Gleichverteilung der Orientierung aller Moleküle im Pressling) mit dem cos2-gemitteten Dipolübergangsmoment:
 |
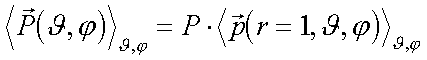(2.1) |
Die Mittelung kann sich dabei auf den Einheitsvektor beschränken.
 |
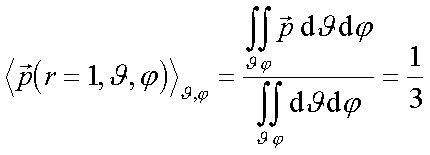(2.2) |
Mittelt man einen Einheitsvektor derart, so ergibt sich 1/3 als Mittelwert. Deshalb erhält man als Extinktionsmeßwert am Pressling nur 1/3 der maximal möglichen Wechselwirkung bei ideal paralleler Orientierung des Dipolübergangsmoments zum E-Vektor. Anders herum kann man aber aus dem Extinktionsmesswert den Betrag des Dipolübergangsmoments (von einem konstanten Faktor abgesehen) bestimmen, indem man den Meßwert einfach mit Drei multipliziert.
Man mißt also das Volumenspektrum am Pressling, berechnet daraus, wie im Kapitel zum Dipolmoment (Gl. 5.3) beschrieben
 |
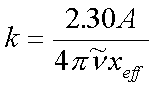A...Extintion (Peakfläche) ...Wellenzahl des Peakmaximumsxeff...effektive Schichtdicke der Einwaage |
(TDM 5.3) |
das isotrope k-Spektrum und multipliziert mit Drei, um den anisotropen Betrag kaniso zu erhalten
 |
(2.3) |
Der Index "aniso" wird im Weiteren weggelassen. Die Orientierung des Vektors im Oberflächen-Koordinaten-System (z = Oberflächennormale) ist dieselbe wie jene des entsprechenden (dynamischen) Dipolübergangsmoment-Vektors, der aus der Orientierung der Molekülgruppe im Moleülkoordinatensystem bekannt ist und in das Oberflächenkoordinatensystem transformiert werden muss. Für die i-te Normalmode gilt
 |
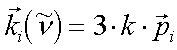(2.4) |
Die x-, y- und z-Komponenten der einzelnen ki ergeben sich in Abhängigkeit von Tiltwinkel qi und Azimutwinkel fi der dynamischen Dipolmomente pi im Oberflächenkoordinatensystem und sind
 |
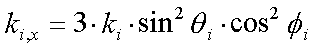(2.5) |
 |
|
 |
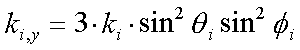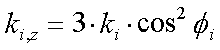An Metalloberflächen ist wegen der Abschirmungwirkung des Metalls nur der Imaginärteil des Films in z-Richtung (normal zur Oberfläche) interessant. Ergibt sich Summe über alle Schwingungsmoden i:
 |
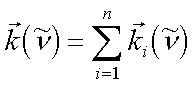(2.6) |
Im Bereich des sichtbaren Lichts ist bekannt, daß blaue Strahlen beim Übergang z. B. von Luft in Glas stärker gebrochen werden als rote. Die Brechkraft des Glases nimmt mit der Energie (der Wellenzahl) des Lichtes sehr langsam zu, es ist dn/dn>0. Diese von Absorptionsbanden entfernt liegenden Bereiche werden als Bereiche normaler Dispersion bezeichnet. In Wellenzahlbereichen, in denen das an seiner Oberfläche brechende Medium absorbiert, fällt der Brechungsindex bei zunehmender Energie rasch ab (dn/dn<0), man spricht von anormaler Dispersion.
Fällt Licht auf die Oberfläche eines absorbierenden Mediums, so ist die reflektierte (und entsprechend die transmittierte) Intensität nicht konstant. Das Reflexionsvermögen einer Grenzfläche hängt vielmehr von den Brechzahlen n (Realteil des komplexen Brechungsindex) beiderseits der Grenzfläche, von der Richtung des E-Vektors (Polarisation) als auch vom Einfallswinkel der optischen Welle ab. Der Betrag des reflektierten E-Felds der Welle bzw. die reflektierte Intensität I werden durch die Fresnelschen Formeln bestimmt, die die genannten Größen beinhalten.
Wieviel Prozent der einfallenden Intensität an den Grenzflächen Luft-Monolayer bzw. Monolayer-Metalloberfläche jeweils reflektiert werden, hängt bei Konstanz von Einfallswinkel und Polarisation vom Realteil n des komplexen Brechungsindex ab. Wäre der Realteil im Bereich der Eigenabsorption des Adsorbates eine Konstante, hätte er keinen Einfluß auf das Spektrum.
Tatsächlich sind jedoch Real- und Imaginärteil des komplexen Brechungsindex miteinander verknüpft und beeinflussen sich gerade im Bereich einer Absorptionsbande stark. Bei einer Änderung des Imaginärteils, ändert sich auch der Realteil. Die Berechnung des Realteils erfolgt dabei mittels der Krames-Kronig-Transformation (sieh unten).
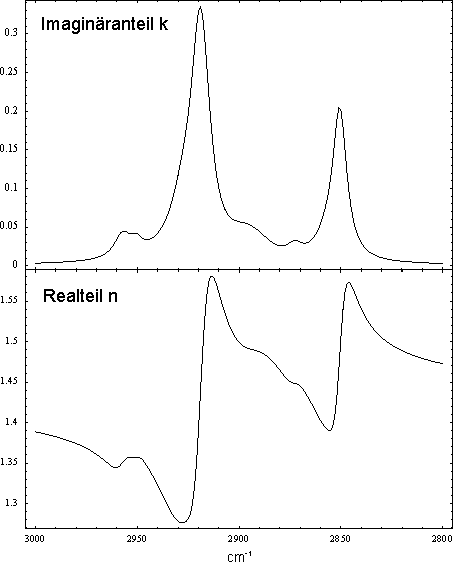
Eine Absorptionsbande eines Monolayers kann daher nie völlig symmetrisch sein, da n und damit die Reflektivität des Adsorbates auf der höherfrequenten Seite der Absorptionsbande kleiner ist als auf niederfrequenten Seite.
Die Kramers-Kronig-Transformationen bezeichnen im Allgemeinen Relationen zwischen Dämpfung und Ausbreitung von Wellen an schwingenden Objekten eines Mediums. Der Zusammenhang ergibt sich daraus, daß Energieaufnahme und ständige (Um-)Polarisation der Moleküle letztlich im Schwingungsverhalten der Moleküle oder -gruppen begründet liegt. Die Dämpfung der Welle durch Schwingungsanregung der Moleküle wird durch den imaginären Teil k des Brechungsindex und die verringerte Ausbreitungsgeschwindigkeit der Welle infolge der verzögert dem E-Feld nachfolgenden (Um-)Polarisation des Mediums durch den realen Teil n des Brechungsindex ausgedrückt. Mit den Krames-Kronig-Transformationen lassen sich Real- und Imaginärteil des Brechungsindes ineinander umrechnen.
Bei optischen Wellen lassen sich durch Anwendung der Kramers-Kronig-Transformationen Real- und Imaginärteil des komplexen Brechungsindex auseinander berechnen. Für die Umrechnung des mittels IR-Speltroskopie gemessenen Imaginärteils in den Realteil lautet die von Kramers und Kroning aufgestellte Relation:
 |
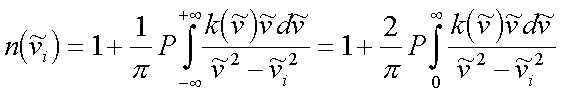(4.1) |
wird vermieden. Gleichung 4.1 besagt, daß der Realteil des Brechungsindex für eine beliebige Wellenzahl berechnet werden kann, wenn der Imaginärteil im gesamten Spektralbereich bekannt ist, Letzteres ist in der Praxis nie der Fall. Man behilft sich, indem man über ein begrenztes, bekanntes Intervall integrert und die "1" in Gleichung 4.1 durch den (annähernd konstanten Brechungsindex n¥ an den Integrationsgrenzen ersetzt.
 |
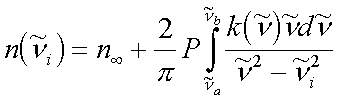(4.2) |
Das Integral kann zur numerischen Integration durch eine Summe ersetzt werden. Die Singularität wird durch den Wegfall des entsprechenden Summanden vermieden.
 |
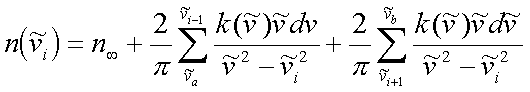(4.3) |
Genau wie der Imaginärteil des Brechungsindex ist auch der Realteil eine vektorielle Größe. Daher müssen die x-,y- und z-Komponenten separat transformiert werden:
 |
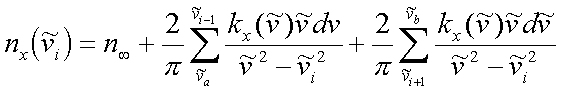(4.4) |
n¥ kann für alle Raumrichtungen als konstant angenommen werden.
Die im nachfolgenden Kapitel genutzte komplexe Dielektrizitätskonstante e berechnet sich zu
 |
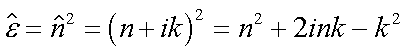(4.5) |
Eine typische Probe besteht aus einem Substratträger, einem aufgedampften Metallfilm und der darauf adsorbierten, orientierten Molekülschicht (nachfolgendes Bild).
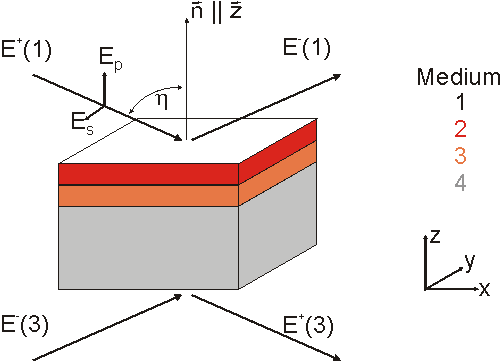
Das elektrischen Feld einer einfallenden optischen Welle zerlegt sich an der Oberfläche in seine parallel bzw. senkrecht zur Einfallsebene polarisierten Komponenten. An jeder Grenzfläche der planparallelen Medien (Schichten) wird es komponentenweise, teilweise reflektiert/transmittiert. Die Partialwellen der elektrischen Feldstärke mit positiver x-Komponente des Wellenvektors k sind mit "+", solche mit negativer mit "-" gekennzeichnet. Zu ermitteln ist das relative Verhältnis der einzelnen E-Feld-Amplituden.
Betrachtet wird nun der Spezialfall nur eines einfallenden Lichtstrahls E+(1), der in der xz-Ebene unter dem Einfallswinkel h auf einen Stapel von 3 planparallelen Medien trifft. Ist, wie in unserem Fall, die Metallschicht mindestens 200 nm dick, so ist sie optisch nicht mehr transparent. Dann kann das Substrat 3 ignoriert und der Metallfilm als unendliches Medium (Halbraum 3) betrachtet werden.
Dann sind alle Komponenten von E(3) gleich null. Damit jedoch die an den Grenzen 1/2 und 2/3 zurückreflektierten Wellen nicht übersehen werden, werden die Partialfelder E(3) dennoch mit aufgeführt: |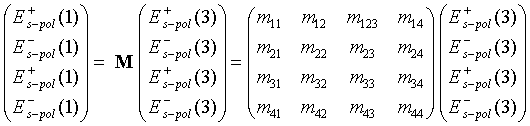
(5.1) |
Die ganze für eine Spektrensimulation notwendige Information steckt dann in den 16 Matrixelementen von M.
Für jede Einzelwelle im jeweiligen Medium gilt die Wellengleichung
 |
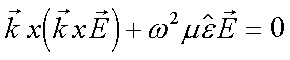(6.1) |
durch 
ersetzen mit er = n2. Der Wellenvektor 
der j-ten Phase hat den Betrag 2p
(j) und zeigt in Ausbreitungsrichtung.
Aus den Maxwellgleichungen ergibt sich eine entscheidende Randbedingung; die x- und y- Komponenten des Wellenvekrors sind in allen Phasen gleich (das ergibt sich aus der Homogenität der einzelnen Phasen, weshalb Lichtwellen ihre Richtung nur an den Phasengrenzflächen ändern und aus der Stetigkeit der Tangentialkomponenten des elektrischen Felds an jeder Grenzfläche).
Im folgenden wird der Wellenvektor (kx, ky, kz) durch (a, b, g) ersetzt. Die Wellengleichung kann dann geschrieben werden als
 |
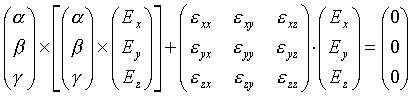(6.2) |
substituiert ist.
Nach Auflösen der Vektorprodukte ergibt sich daraus
 |
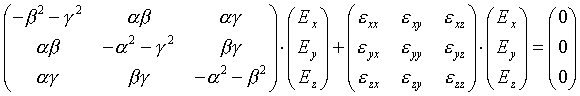(6.3) |
 |
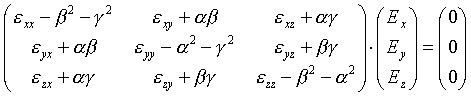(6.3a) |
Für jede nichttriviale Lösung muß die Determinante der Koeffizientenmatrix Null sein. a und b sind konstant (siehe oben) und durch Einfallswinkel und -ebene vorgegeben.
Im hier betrachteten Spezielfall liegt der einfallenden Strahl in der xz- Ebene, deshalb ist b gleich null. In einer weiteren Vereinfachung beschränken wir uns auf uniaxiale Medien. Dieser Fall ist durch die Symmetrie des Metallfilms erfüllt: Das einfallende IR-Licht beleuchtet die Probe im Bereich einiger Millimeter. Hat nun ein monokristallines Substrat (Metall-Einkristall) eine mindestens dreizählige Symmetrie oder ist des Substrat polykristallin (zufällige Orientierung der Kristallite), so sind durch Mittelungen des IR-Lichts über makroskopische Oberflächenbereiche dessen Eigenschaften in x- und y-Richtung gleich, es lassen sich nur noch die Richungen senkrecht und parallel zur Oberfläche unterscheiden. Gleiches gilt dann für den selbstordnend aufgebrachten, zu untersuchenden Film (SAM). Der dielektrische Tensor e = besitzt dann die Gestalt einer Diagonalmatrix, alle Mischlieder eij mit i¹j verschwinden. Gleichung 6.3 vereinfacht sich dann zu
 |
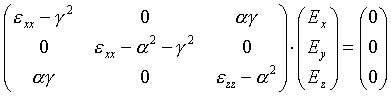(6.4) |
Gesucht werden folglich für jede einzelne, durch e (j) charakterisierte Schicht j alle Werte g (j), für die die Determinante der Matrix in Gl. 6.4 gleich Null wird. Es ergibt sich eine Gleichung vierten Grades, zu der es nach dem Fundamentalsatz der Algebra genau 4 komplexe Lösungen gibt. Für ein nicht absorbierendes Medium (e reell) ergeben sich nur reelle Lösungen. Für ein uniaxiales, absorbierendes Medium erhält man zwei Lösungen, die jeweils einen positiven bzw. negativen Realteil (entspricht den hin- bzw. rücklaufenden Wellen) und einen betragsmäßig gleichen Imaginärteil (identische Dämpfung für hin- und rücklaufende Wellen) haben:
 |
(Lösung für s-pol. E-Feld) | (6.5) |
 |
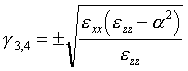(Lösung für p-pol. E-Feld) |
Die zu den einzelnen Partialwellen ks,j (s = 1,2,3,4, s ...Index der Lösung, j...Index der Schicht) gehörende Polarisierungsrichtung des elektrischen Feldes läßt sich aus den Kofaktoren (der Kofaktor einer Zeile ist das Kreuzprodukt der beiden anderen Zeilen) der Koeffizientenmatrix in Gleichung (6.4) ermitteln. Das ergibt sich aus der Überlegung, daß jeder der drei Zeilenvektoren dieser Matrix zum Feldvektor E senkrecht steht, da deren Vektorprodukt jeweils gleich null ist:
 |
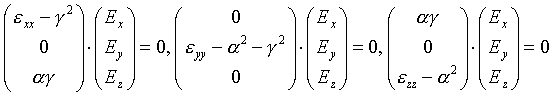(6.6) |
Das Vektorprodukt zweier Zeilenvektoren steht zu diesen ebenfalls senkrecht. Wenn nun die Zeilenvektoren zueinander und zu 
senkrecht stehen, muß das Kreuzprodukt parallel zu orientiert sein, der Kovektor einer Zeile der Koeffizientenmatrix in Gl. 6.4 ist also der Polarisation der Welle parallel. Dabei genügt es einen Kovektor zu berechnen. Der Kovektor für Lösung 1 im Medium 2 lautet zum Beispiel
 , |
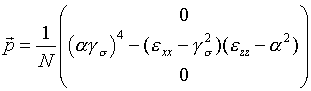(6.7) |
Lösung 1 im Medium 2 beschreibt eine s-polarisierte Welle. Der Vorfaktor 1/N dient der Normierung und folgt aus p2:=1. Da sich Lösung 2 im Medium 2 nur im Vorzeichen unterscheidet, besitzt der Polarisationsvektor die gleiche Orientierung, er beschreibt die zweite s-polarisierte Welle. Weil die zweite Zeile der Koeffizientenmatrix in Gl. 6.4 für die Lösungen g1,2 nur Nullen enthält, liefern der erste und dritte Kofakor in diesem Fall keine Lösungen. Allein der normierte Kofaktor der zweiten Zeile (wie oben berechnet) gibt einen Einheitsvektor parallel zur y-Achse (Gl. 9.7). Entsprechend müssen die Lösungen g 3,4 zum p-polarisierten elektrischen Feld gehören des Mediums 2 gehören. Der Kofaktor der zweiten Zeile liefert hier ein falsches Ergebnis (Parihk, Allara, J. Chem. Phys. 96 (1992)2, Fußnote 95). Allein die Kofaktoren der ersten bzw. dritten Zeile ergeben die richtige Polarisierung.
Anmerkung: In isotropen Medien (exx = eyy = ezz) liefert auch der Kofaktor der zweiten Zeile für g1,2 einen Nullvektor, die s-Polarisation muß dann manuell vorgegeben werden. Auch die Kofaktoren der ersten und dritten Zeile sind dann null, die Richtung des p-polarisierten Feldvektors kann ebenfalls nicht mehr aus den entsprechenden Kofaktoren ermittelt werden kann. Stattdessen wurden für isotrope Medien (Vakuum, Substrat) die Kreuzprodukte eines Einheitsvektors in y-Richtung mit den Wellenvektoren k3,4 gebildet.
Zwischen den vier partiellen elektrischen Feldern der Lösung eines Mediums und den entsprechenden magnetischen Feldern gilt die Beziehung
 |
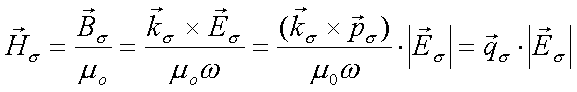(6.8) |
mit
 . |
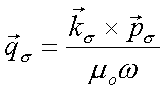(6.8a) |
Wenn für jede Phase j die jeweils vier 
bestimmt sind, müssen diese vor Anwendung der Matrixmethode noch sortiert werden. Damit sich später symmetrische Matrizen ergeben, bekommt
 . |
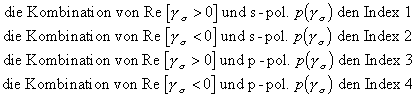(6.9) |
Als erste 4x4-Matrix soll die sogenannte Propagation Matrix (Ausbreitungsmatrix) konstruiert werden. Sie beschreibt, wie sich die E-Feldamplituden As der vier Lösungen entlang der z-Achse innerhalb einer homogenen Schicht j der Dicke t(j) ändern. Die Propagation Matrix P(j) hat die Form
 |
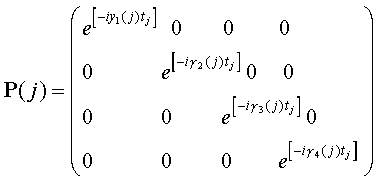(7.1) |
mit
 . |
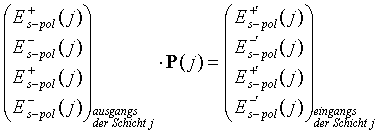(7.2) |
Die Maxwellgleichungen fordern die Konstanz der Tangentialkomponenten von elektrischem und magnetischem Feld E und H an allen Grenzflächen. Da E und H jeweils die Summe der vier partiellen E- und H-Felder (der vier Lösungen pro Medium) ist, folgt daraus, daß die Summen der Tangentialkomponenten ausgangs der (j-1)-ten und eingangs der j-ten Phase gleich sein müssen.
 . |
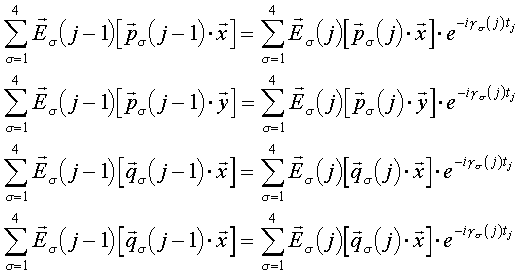(7.3) |
(Es ist H = Eq nach Gl. 6.6, d.h. Gl. 7.3 beschreibt die Stetigkeit der E- und der H-Felder der s- und p-polarisierten Wellen)
Diese Randbedingungen lauten in Matrixform ausgedrückt:
 |
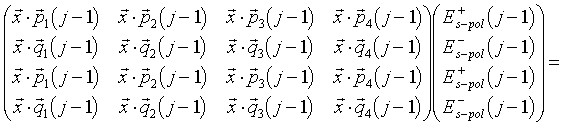(7.4) |
 |
|
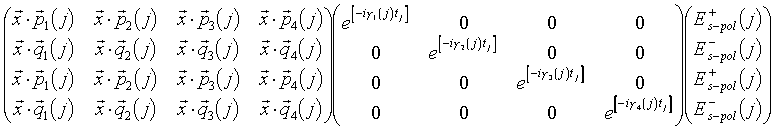Mit der Definition der dynamischen Matrix D(j)
 |
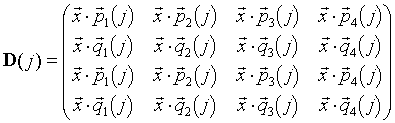(7.5) |
verkürzt sich Gl. 7.4 zu
 |
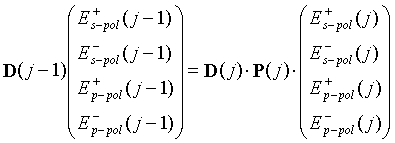(7.6) |
oder
 |
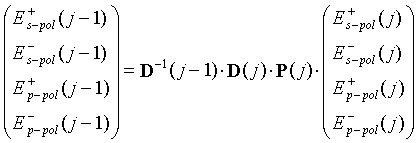(7.7) |
= |
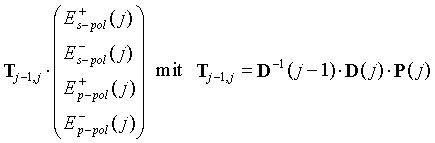Durch Multiplikation der einzelnen Transfermatrizen kann man nun auch für alle Schichten das Verhältnis der partiellen Feldamplituden berechnen:
 |
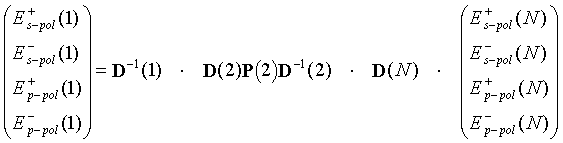(7.7) |
Die in Gleichung 6.1 definierte 4x4 Matrix M
|
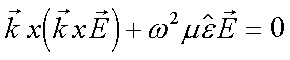(6.1) |
ist demnach das Produkt aller Transfermatrizen:
| M = T1,2 T2,3 | (7.8) |
Die Reflexionskoeffizienten r des gesamten Schichtsystems hängen jeweils nur von einem Teil der insgesamt 16 Matrixelemente mij ab:
 |
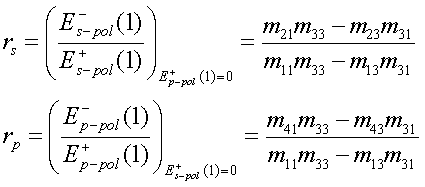(8.1) |
Die Reflektivität R ergibt sich zu
| R = r r*. | (8.2) |
Zur Spektrensimulation rechnet man die Reflektivität jeweils getrennt für den Fall des unbeschichteten (Ro) bzw. beschichteten Substrats (R) und errechnet daraus das IR-Spektrum des Filmes
| A = lg(Ro/R). | (8.3) |
|
|
 Impressum |
Fragen, Hinweise, Kritiken:
ralf@arnolds.de |